The objective of my research is to tackle open problems in Strongly Correlated Matter by developing novel numerical algorithms bridging the gap between Machine Learning (ML) and Quantum Physics, and to apply them to the study of Strongly Correlated Matter.
My interest is especially centered around matter driven out of equilibrium such as Open Quantum Systems.
I am looking for motivated students to do their Master internship or PhD with me. If you are already a researcher somewhere and wish to collaborate, drop me an email!
Neural-Network Quantum States
Quantum Mechanical Systems involve an exponentially-increasing number of coupled degrees of freedom which quickly becomes intractable to classical computational methods. Over the years, many computational techniques have been developed to avoid such cost, ranging from Tensor Network methods to Quantum Monte Carlo.
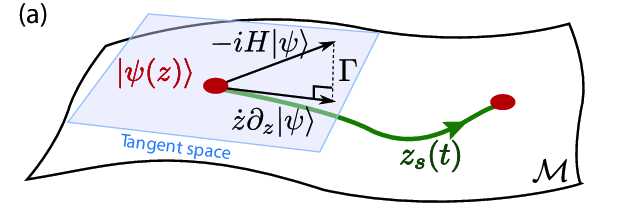
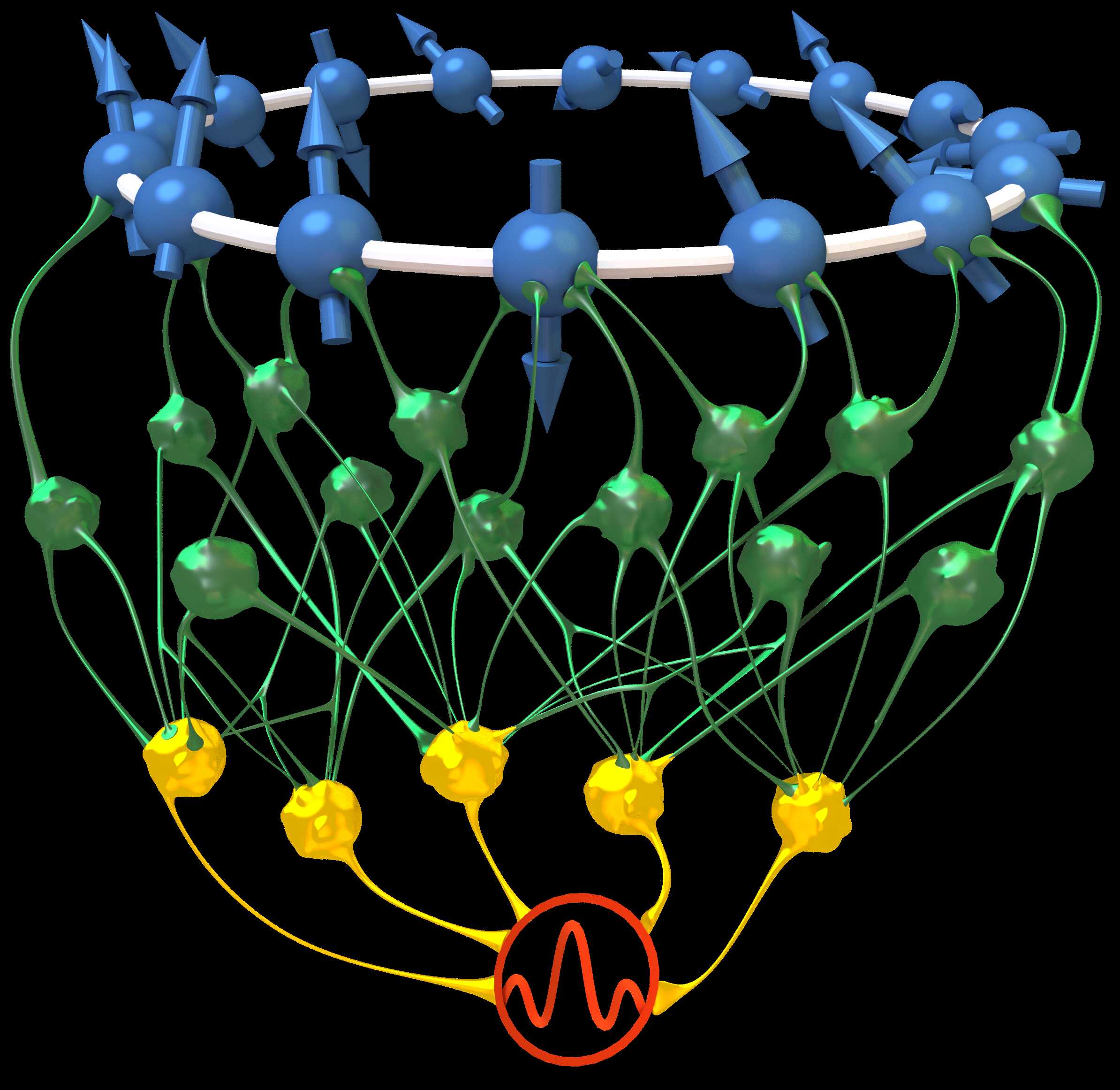
A particularly succesful idea has been that of interpreting the state of a quantum system as an unknown functional that can be approximated by a Neural-Network.
The parameters of the neural-network must be optimised using some iterative algorithm such as stochastic-gradient-descent or ADAM. However, as the underlying physical principles are known, it has been possible to devise algorithms that avoid many of the complications of standard artificial intelligence tasks and give extremely accurate results.
I call this approach Knowledge-driven Machine Learning, as opposed to the Data-Driven approach that is commonly considered.
Within the domain of Computational Physics, the selling point of Neural Quantum States (NQS) methods is their ability to represent states in 2- and 3-Dimensional systems, which cannot be easily tackled with Tensor Networks. Moreover, NQS methods avoid the so-called sign problem. I have also shown how to use NQS to study “Open” Quantum Systems, where the noisy environment decoheres the quantum state and forces us to use a classical mixture to describe the state. Thanks to this, it is now possible to simulate large quantum experiments using NQS techniques.
The success of Neural Networks as state approimators also owes to our understanding of physical simmetries: by devising Architectures that implicitly enforce them we are able to obtain very accurate results. While lattice symmetries such as translations and rotations are relatively simple to enforce, it is not yet clear how to constraint nonlinear ansatzes to respect a more complicated constraint, such as those arising from the
Of course, there is no free lunch, and the exceptional representational power of Neural Networks comes at a price: an highly nonlinear optimisation problem. The optimisation problems that arise with NQS are non-trivial, and there’s a strong interest into developing advanced, higher-order optimisation schemes that can converge more efficiently to the desired state.
It is for that reason that I strongly believe that, in order for NQS to overtake the world become a viable, first-class algorithm we need to devise more controlled, adaptive schemes that can automatically detect errors and correct for them. In the meantime, while we wait for the next scientist to revolutionise the field even more, there are also many other open questions…
For example, a very succesful direction is that of the natural gradient (pun intended), which leverages ideas from differential geometry such as the curvature tensor associated to a neural network. This object, the so-called Quantum Geometric Tensor, has several properties that are also of interest in the domain of Variational Quantum Algorithms, where many articles have investigated its properties
Open Quantum Systems
Channeling the power of quantum mechanics is within the reach of actual technological paradigms, paving the road to the fabrication of large-scale quantum devices, but it is also necessary to protect the fragile quantum state of such devices. The inevitable relaxation to thermal equilibrium is traditionally avoided by isolating quantum devices from the environment. Yet, despite the tremendous experimental progress a finite coupling to the environment is unavoidable and certainly plays a crucial role in the practical implementation of quantum information and quantum simulation protocols.
By improving our microscopical models of those devices to account for their dissipative nature it would be possible to improve the fidelity of their operations, to devise new experimental protocols, or even to design innovative devices. One of the most estabilished frameworks to treat dissipative systems is the Lindblad Master Equation, which accounts for the interaction with the environment.
Unfortunately, while integrating the Schroedinger’s equation is already hard, solving the Lindblad Master Equation is even harder. Not only it involves evolving an object, the density matrix, which has more degrees of freedom, but it also involves matrices with less structure. For example, while the Hamiltonian is hermitian and therefore can be accurately diagonalised or used to build a Krylov space to study the time-evolution, the Liouvillian is non-hermitian and therefore many numerical issues eventually appear.
It is for that reason that novel numerical tools might be particularly useful to answer open questions within the domain of Open Quantum Systems. And Neural Quantum States are one such numerical technique I have been investigating. The main challenge to their development is the fact that the density matrix has a lot of structure, such as a positive spectrum, that is hard to enforce through a Neural-Network description. Over the years, I’ve been working to find ways to devise better, more expressive, variational encodings for the density matrix.